
Zagraj w Futoshiki Puzzle Online
W poniższym samouczku, podstawowe i zaawansowane techniki rozwiązywania zagadek Futoshiki są przedstawiane krok po kroku, wraz z towarzyszącymi ilustracjami przedstawiającymi metody na określonych konfiguracjach płyt.
Punktem wyjścia do rozwiązania jest definicja samej gry: Futoshiki wymaga od użytkownika znalezienia planszy, na której każda cyfra pojawia się raz w każdym rzędzie i kolumnie, szanując nierówności tablic. Stosując to kryterium, postęp w kierunku rozwiązania można dokonać, wypełniając, krok po kroku, puste kwadraty planszy z określonymi cyframi, ponieważ są one jedynym sposobem przestrzegania ograniczeń tablic.
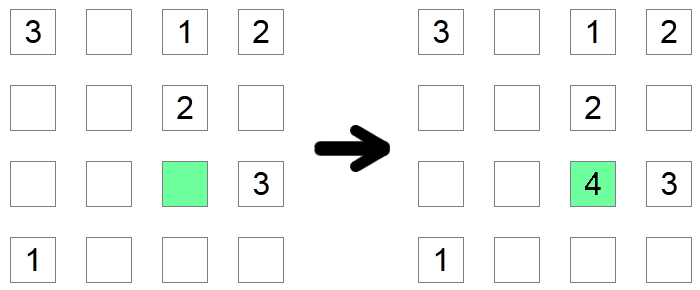
Jeśli kolumna i wiersz kwadratów zawierają już wszystkie możliwe cyfry, z wyjątkiem jednej, to ten kwadrat musi zawierać brakującą cyfrę. W powyższym przykładzie zielony kwadrat musi wynosić 4, ponieważ nie byłoby dozwolone posiadanie żadnej innej wartości, ponieważ inne możliwe cyfry znajdują się już w jego wierszu lub kolumnie.
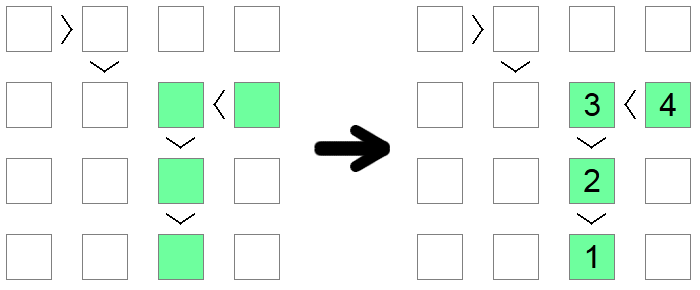
Jeśli zauważysz łańcuch nierówności, czy to < (wszystkie rosnąco), czy > (wszystkie malejące), równe rozmiarowi z rozmiarem desek, to ten łańcuch musi być sekwencją od 1 do długości planszy. Długość łańcucha gwarantuje, że ta sekwencja jest jedynym możliwym rozwiązaniem, które spełnia monotonny warunek narzucony przez łańcuch nierówności.
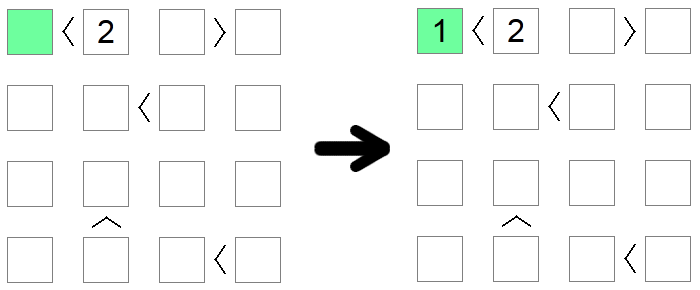
Kwadraty, które są mniejsze niż 2 muszą domyślnie mieć wartość 1, ponieważ jest to jedyna dopuszczalna wartość na tablicy, która przestrzega tego warunku. Podobnie kwadraty, które są większe niż rozmiar płyty minus 1, muszą być równe rozmiarowi planszy. W powyższym przykładzie jedyną możliwą wartością dla zielonego kwadratu (mniej niż 2) jest 1.
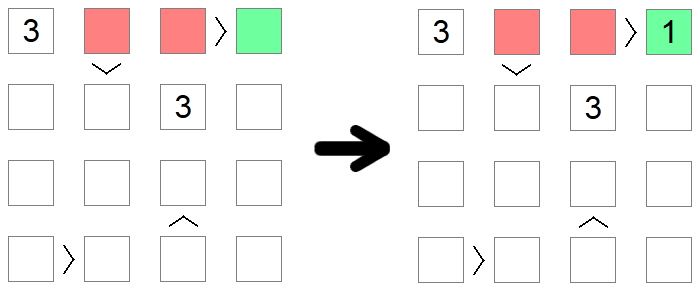
Kwadraty większe niż inne kwadraty nie mogą być 1, najniższa wartość dozwolona na planszy, ponieważ nie ma wartości mniejszej niż 1. Podobnie kwadraty niższe niż inne kwadraty nie mogą zawierać maksymalnej dozwolonej wartości, ponieważ po drugiej stronie nierówności nie byłoby nic większego do wypełnienia. W powyższym przykładzie 1 nie można wypełnić czerwonych kwadratów, ponieważ wszystkie są większe niż inne kwadraty planszy, więc jedynym możliwym umieszczeniem dla 1 w pierwszym rzędzie planszy jest zielony kwadrat.
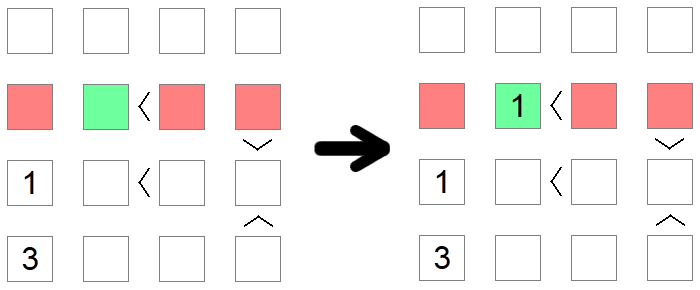
Czasami trzeba użyć wielu reguł, aby dojść do wniosku. Tak jest w powyższym przykładzie, w którym staramy się umieścić wartość 1 w drugim rzędzie planszy. Pierwszy czerwony kwadrat jest eliminowany z powodu wykluczenia kolumny (mamy już 1 na tej kolumnie), podczas gdy drugi i trzeci czerwony kwadrat są eliminowane z powodu wykluczenia wartości minimalnych, ponieważ miejsca te mają większe niż związane z nimi nierówności. Dlatego zielony kwadrat pozostaje jedynym możliwym miejscem do umieszczenia 1 w tym rzędzie.
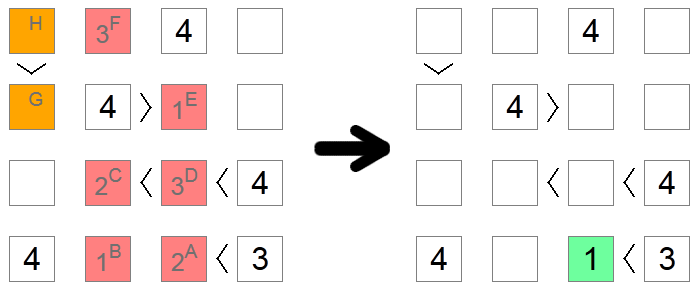
Czasami, zwłaszcza na trudnych deskach, nie ma innych sposobów na ustalenie prawidłowej cyfry kwadratu, z wyjątkiem zanurzenia się w implikacjach każdej możliwości, dopóki nie zostanie osiągnięta sprzeczność. W powyższym przykładzie wszystkie czerwone i pomarańczowe kwadraty są początkowo puste. Chcemy dowiedzieć się, czy kwadrat A zawiera 1 lub 2. Zakładamy, że zawiera 2 i sprawdzamy, czy osiągniemy sprzeczność w oparciu o to założenie.
Jeśli kwadrat A ma 2, to kwadrat B miałby 1 (jedyną pozostałą wartość w dolnym rzędzie). Kwadrat C może wynosić 1 lub 2, ponieważ ma łańcuch nierówności, który wymaga posiadania 2 większych liczb, ale teraz nie może być 1 ze względu na wykluczenie kolumny kwadratu B, więc kwadrat C to 2, a kwadrat D to 3 (jedyna wartość między 2 a 4). Ze względu na wykluczenia kolumn, kwadrat E to 1, a kwadrat F to 3.
Teraz, jeśli spojrzymy na pomarańczowe kwadraty, zauważamy sprzeczność: gdyby kwadrat G miał wynosić 2, kwadrat H musiałby wynosić 3 lub 4, które nie są dozwolone z powodu wykluczenia rzędu. Gdyby kwadrat G miał być 3, kwadrat H musiałby być 4 co nie jest dozwolone z tego samego powodu. Ponieważ nie mamy już pozostałych wartości kwadratu G, oznacza to, że osiągnęliśmy impas i nasze początkowe założenie było błędne: 2 nie jest prawidłowym ruchem dla kwadratu A, więc możemy iść dalej i umieścić w nim 1, jedyną inną możliwą wartość.
Pokazaliśmy powyżej, jak skutecznie rozwiązać zagadkę Futoshiki, obejmując szereg technik, które pomogą Ci wydedukować następny ruch nawet w trudnych sytuacjach. Innym kluczowym składnikiem biegłości i szybkiego rozwiązywania zagadek Futoshiki jest doświadczenie: im więcej ćwiczysz, tym lepiej i szybciej się staniesz.
Jeśli jesteś na wyzwanie, możesz teraz zagrać w losową układankę Futoshiki, klikając poniższy przycisk. Powodzenia!
© 2026 - Wszelkie prawa zastrzeżone - O - Polityka prywatności - DE | EN | ES | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR